Здравейте, Юлиянg да абсолютно сте прав за точността на измерванията и ви подкрепям на 100%, но въпроса тук, който повдигна Бат Ванко и Пикси преди него е по фундаментален.
Става дума за фундаментални математически грешки допуснати още преди 200-300 години на зората на зараждащата се тогава днес наука Електроника за електричеството и магнетизъма.
Въпроса е повдигнат, че нали ние тук във МАЗЕТО форум за свободна енергия това търсим от години, а именно грешките допуснати във физиката.
Повечето грешки откривани досега са направени само от математици с принос към Физиката, които опростявайки формулите на физичните явления и привеждайки ги под общ знаменател например, математически те са верни, но реално се пренебрегват смисъла на физиката и явленията, които стоят зад тях, също така и редица от реалните експерименти и резултати от опитите през столетията после, през годините изминали до днес, неудобните практически факти и експерименти, са замитани под килима и прикривани умело и виртуозно математически. Няма в нито един учебник днес да срещнете физичен опит или експеримент, който противоречи на теорията, а в началото е имало доста такива, като изключения от теорията са давани, като теми за по-дълбок размисъл, но с времето от добри намерения постепенно са премахнати всички неудобни истини, уж по съвсем други оправдания например безобидните: за липса на обем в учебника и/или съкращаване на материала за обучение, колко удобно нали.
И така днес имаме стройна система SI, разбира се без СЕ, а това не е обективната истина.
Предлагается другая альтернативная концепция - "Энергия электрического импульса тока (напряжения) - неисчерпаема", которая решает абсолютно все энергетические проблемы наших дней и будущего.
Так принято, и это разумно, что научная этика требует, прежде чем утверждать, что ошибся предшественник, искать ошибку у себя. В данном случае у себя все проверено и ошибки исключены.
Вот элементарный пример:
1 + 1 = 2. (1)
Получен первичный изначальный результат - два. Научная мысль расценила, что такое равенство не годится для высшей математики и значение два здесь слишком много. Поэтому левую и правую части равенства 1 разделили на два, т. е.
1/2 + 1/2 = 1. (2)
Казалось бы, арифметическое действие здесь не запрещено математикой и поэтому оба равенства считаются равнозначными. Однако все это не так просто. Представим левые значения равенств - это коэффициенты, определяемые амплитуды сигналов. Возведем в квадрат оба равенства, получаем в первом случае
(1 + 1)2 = 4 (3)
и во втором случае
(1/2 + 1/2)2 = 1. (4)
Следовательно, в результате деления левой и правой частей равенства его значение уменьшается в четыре раза. В пересчете на сигналы мощность сигнала будет уменьшена в четыре раза или по уровню мощности на - 6,0 дБ.
Это чрезвычайно большая потеря.
Первоклассные ученые прошлого сделали все возможное, чтобы не допустить первый результат и направить математическую физику по второму результату.
Леонард Эйлер (1707-1783) - швейцарец по происхождению, филолог по образованию, долгое время жил в России, стал великим математиком, физиком, механиком, астрономом - основной участник спора, совместно с Даламбером и Лагранжем по вопросу о возможности разложения заданной функции в тригонометрический ряд ввел формулу, носящую его имя

из которого формула Эйлера была получена путем деления левой и правой частей равенства 6. Эта грубейшая ошибка существует в математической физике около 250 лет с середины XVIII в. и доминирует в фундаментальных соотношениях основ теории спектров радиотехнических сигналов. Так, тригонометрический ряд Фурье был определен делением левой и правой частей исходного равенства на два
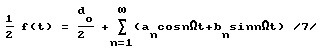
где ao, an, bn - коэффициенты Эйлера-Фурье, 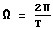 , t - время, что привело к расходимости ряда, так как снижает амплитуду исходного сигнала в два раза, или по мощности в четыре раза, или по уровню мощности на - 6,0 дБ вместо сходящегося Обратного ряда Фурье
, t - время, что привело к расходимости ряда, так как снижает амплитуду исходного сигнала в два раза, или по мощности в четыре раза, или по уровню мощности на - 6,0 дБ вместо сходящегося Обратного ряда Фурье

Общеизвестное ядро Дирихле
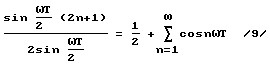
получено делением левой и правой частей следующего равенства
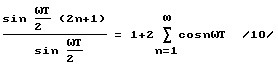
на два, что привело к катастрофическим последствиям. Также с такой ошибкой существуют до сих пор интеграл Дирихле, интеграл Фурье и многие другие полезные для практики формулы.