Източник:
http://macmep.h12.ru/meg.htm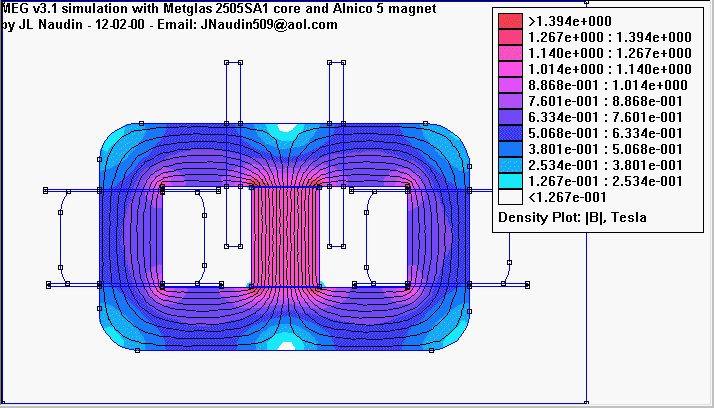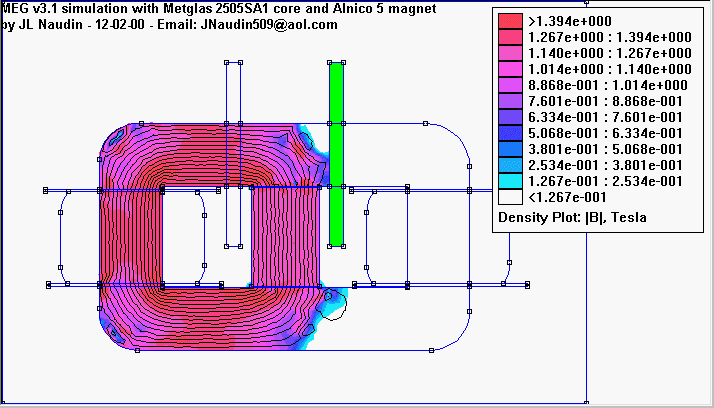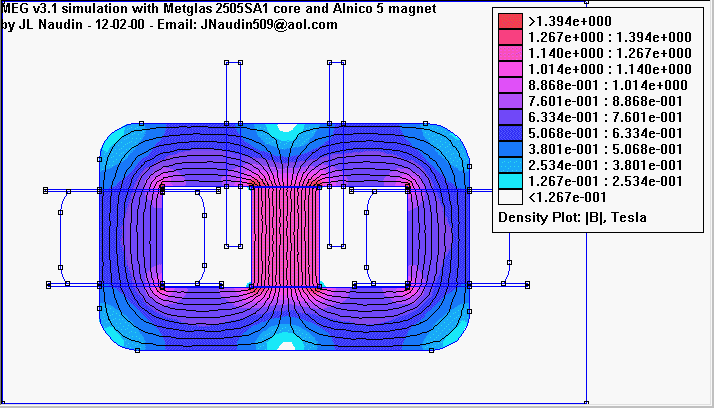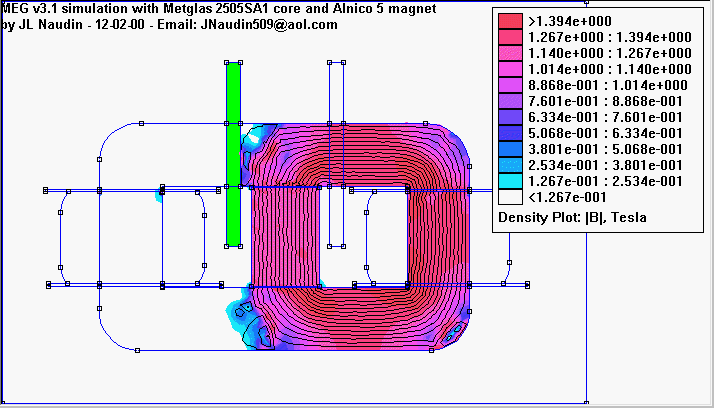 Комментарии:
Комментарии:Рассмотрим пока работу без нагрузки. Возьмём просто сердечник. В нём нет полей. Напряжённость поля - 0. Теперь вставим в середину магнит - его поле распределится поровну в каждой половине сердечника (половина, это то, что слева и справа от магнита). Магнит нужно взять такой силы, чтобы он создал в сердечнике напряжённость магнитного поля, равную половине напряжённости насыщения для данного сердечника. Или подобрать зазоры между магнитом и сердечником, или между сердечниками, для достижения той же цели.
Наудин взял пермалоевый сердечник с насыщением - 1,5 Тесла. В принципе, это почти предел для пермаллоя. Его не то, что превышать, достигать нельзя. Напомню, с насыщением сердечника нужно бороться. Насыщение для MEG-а - лишняя трата энергии.
Поставив магнит, обеспечивающий напряжённость поля примерно 1,37 Тл, в сердечнике образуем поле, напряжённостью 1,37/2=0,68 Тл.Посмотрите на рисунок в переведенной статье принципа работы MEG-а. Это тот рисунок, в котором весь сердечник синий, а магнит в центре - красный. Цветом обозначена величина напряжённости поля. Правее на рисунке - таблица соответствия цвета и напряжённости поля. На рисунке среднее значение напряжённости 0,5-0,6 Тл. Это установившееся состояние.
Выходные катушки "молчат" - на них напряжение отсутствует.
Теперь расположим управляющие катушки - в верхней части сердечника по обе стороны от магнита. Нужно учесть только, что катушки должны быть соединены между собой (последовательно) так, чтобы при подаче напряжения на каждую катушку поле, созданное этой катушкой было направлено навстречу полю магнита в этой половине сердечника - катушка должна перекрывать поток от магнита! Иначе работать не будет. Вернее, работать-то будет, но как обычный трансформатор, только с постоянным подмагничиванием.
Естественно, ни о каком КПД>1, в таком случае, речи быть не может.
Теперь подадим напряжение на катушку, расположенную слева от магнита. Она поставит затор полю магнита в этой половине (левой) сердечника. В результате, поле магнита перераспределится: целиком (условно) уйдёт в правую половину, создавая там напряжённость, максимальную для магнита (1,37 Тл). При этом, в левой половине сердечника поле, наоборот ослабеет почти до нуля.
При этом в каждой выходной катушке будут наводиться ЭДС, равные по величине, но противоположные по знаку.
На осциллографе это будет выглядеть как две синусоиды, увеличивающиеся от нуля до максимума плюс (правая катушка) и от нуля до максимума минус (левая катушка).
После того как поле установится (это тот рисунок в статье, где левая половина сердечника - белая, а правая - красная), прекратится наведение ЭДС. В левой половине сердечника напряжённость поля почти равна нулю, а в правой - величине, которую в состоянии обеспечить магнит. В данном случае 1,37 Тл. В этом случае синусоида достигает максимальной амплитуды. Это - первая четверть периода работы.
Этот момент нужно не упустить, и выключить первую катушку. Для чего? Для того, что бы не расходовать лишнюю энергию. Как это сделать? Подобрать длительность открытого состояния транзистора, управляющего данной катушкой. Это время зависит от материала сердечника, силы магнита, думаю, что и от параметров управляющей и выходной катушек. В общем, может потребоваться подбор для каждого конкретного устройства. Для второй катушки этот параметр будет таким же. Значит, достаточно будет подобрать оптимальную частоту управления для данного сердечника, катушек и магнита, и коэффициент заполнения импульсов управления с целью минимизации мощности потребления.
В Наудиновских экспериментах указывается, что коэффициент заполнения импульсов выбирается равным 0,5. А в своих комментариях, Сквир рекомендует: ': изменение коэффициента заполнения импульсов управления могло бы помочь уменьшить потребляемую мощность'.
Я пока принимаю этот параметр на уровне 0,25 или четверть периода - половина от максимального 0,5. А в процессе наладки можно будет подобрать наилучшую величину.
Теперь выключаем левую катушку (и подключаем нагрузку). Поле магнита опять начнёт перераспределяться, равномерно заполняя сердечник. При этом, в левой половине сердечника напряжённость растёт от нуля до 0,5-0,6 Тл, а в правой спадает от 1,37 Тл до 0,5-0,6 Тл.
Картинка соответствует той, где сердечник весь синий.
При этом ЭДС, наводимые в выходных катушках будут: в левой - уменьшаться от максимума минус до нуля, а в правой - от максимума плюс до нуля. Это вторая четверть периода, или половина периода.
Обратите внимание: катушки выключены, а магнитный поток сам распределяется по сердечнику, формируя при этом вторую четверть выходного напряжения.
Теперь включается вторая катушка, расположенная справа от магнита (нагрузка выключается). Поле, которое она создаёт, направлено навстречу полю магнита в правой половине сердечника. Поток магнита начнёт перераспределяться, уменьшаясь в правой половине сердечника почти до нуля, и возрастая в левой половине, пока не достигнет максимального уровня, обеспечиваемого магнитом - 1,37 Тл в нашем примере. При этом, в выходных катушках будет снова наводиться ЭДС, но полярность её изменится - в левой напряжение будет расти от нуля до максимума плюс, а в правой - от нуля до максимума минус. К моменту завершения этого процесса, завершится и формирование третьей четверти периода. Это состояние соответствует картинке, где левая половина сердечника красная, а правая - белая.
Так как частота и скважность импульсов у нас уже оптимизированы (конец первой четверти формирования синусоиды), то в этот момент выключается правая управляющая катушка (и снова подключается нагрузка). Поле магнита снова начнёт перераспределяться, возвращаясь в исходное состояние - равномерно заполняя сердечник. И опять без нашей помощи - на это мы не тратим мощность. При этом, в левой половине сердечника напряжённость поля будет уменьшаться с 1,37 Тл до 0,5-0,6 Тл, а в правой половине сердечника - увеличиваться от нуля до 0,5-0,6 Тл, пока не сравняются. При этом в выходных катушках будет формироваться последняя четверть выходного напряжения: в левой катушке уменьшаясь от максимума плюс до нуля, а в правой - от максимума минус до нуля.
Всё. Период завершился. Дальше всё повторяется с начала.
Краткий вывод. Если разделить один период работы MEG-а на четыре части, то в первой и третьей частях мы затрачиваем мощность на переключение потока магнита то в одну половину сердечника, то в другую. Нагрузка при этом отключена. Вторую и четвёртую четверти периода магнит сам выравнивает напряжённость поля в сердечнике. Управляющие катушки при этом обесточены, значит, нет потребления мощности. Но нагрузка подключена, и в ней выделяется полезная мощность.
Теперь рассмотрим подключение нагрузки. Так как нагрузка, подключенная непосредственно к выходным катушкам MEG-а, должна быть нелинейной, то в начале рассмотрим, в чём эта нелинейность заключается.
Наудин рекомендует два варианта: специально подготовленный (кондиционированный) угольный резистор или обычный варистор. Для демонстрации он использует также компактную лампу (газоразрядную) дневного света.
Способ доведения до 'кондиции' обычного объёмного угольного резистора заключается в том, что бы пропустить через него ток высокой частоты (80 кГц) от источника высокого напряжения (киловольты) через разрядник - воздушный промежуток около 6 мм. После такой операции сопротивление резистора увеличивается на порядок, и становится нелинейным. Его сопротивление постоянному току велико, а переменному току высокого напряжения - мало.
Наудин рекомендует, почему-то, брать резистор на 100 Ком.
Несмотря на интересный эффект, практическое применение такой нагрузки, думается , ценности не представляет.
Теперь варистор - нелинейный полупроводниковый резистор, используемый, обычно, в качестве ограничителя выбросов напряжения.
Его сопротивление зависит от напряжения на нём: при малом напряжении его сопротивление велико. При увеличении напряжения его сопротивление начинает уменьшаться, достигая своего некоторого минимального значения при достижении напряжением уровня, установленного для данного варистора.
Раз варистор считается приемлемой нагрузкой для MEG-а, то сделаем вывод: нелинейность нагрузки для MEG-а заключается в том, что с повышением амплитуды выходного напряжения, сопротивление нагрузки должно уменьшается, и, наоборот - с понижением амплитуды сопротивление должно увеличиваться. Так как конкретных рекомендаций и зависимостей нет, то можно предположить, что главное - соблюдать ход этой зависимости.
Пример тому - использование в качестве нагрузки газоразрядной лампы. Пока напряжение на ней не достигнет напряжения пробоя газа, лампа не светит, и её сопротивление, практически, бесконечно большое. При разряде ток через лампу увеличивается, а напряжение на ней падает. Ток должен быть ограничен уровнем, конкретным для данной лампы (в зависимости от мощности).
В экспериментах Наудина лампа подключена напрямую к выходным катушкам, без ограничителя тока. В принципе, это тоже можно объяснить.
Видимо MEG имеет мягкую выходную характеристику. Сопротивление и индуктивность выходных катушек довольно большие.
Однако нас эти нагрузки мало интересуют (разве что лампа). Нам нужно подключать активную линейную нагрузку.
Посмотрите патент Бирдена. В нём указана обычная нагрузка, подключаемая к выходным катушкам через выпрямитель, фильтр и стабилизатор. Стабилизатор, думаю, не изменяет характер нагрузки для MEG-а, хотя его можно заставить это делать. Выходит, что весь секрет заключается в выпрямителе и фильтре. Выпрямитель - понятно. Это набор диодов. А фильтр - сглаживает пульсации выпрямленного напряжения. Основной (и достаточной) деталью фильтра является конденсатор, о котором ещё говорят: конденсатор фильтра. С учётом того, что в патенте указано одно устройство с надписью выпрямитель и фильтр, то можно предположить, что имеется в виду именно выпрямитель с конденсатором фильтра.
Почему мы акцентируем внимание на этом? Потому, что выпрямитель с конденсатором фильтра имеет зависимость входного сопротивления от приложенного напряжения, нужную нам.
Дело в том, что выпрямитель, 'работающий на фильтр с емкостной реакцией, в отличие от других (с индуктивной или чисто активной) работает с отсечкой тока. Величина отсечки характеризуется так называемым углом отсечки, равным половине угла, соответствующего времени прохождения тока через вентиль'.
(Цитата взята из умной старой книги, и поэтому заключена в кавычки.)
Рассматривать работу такого выпрямителя лучше с момента, когда MEG уже работает некоторое время, достаточное для зарядки конденсатора фильтра.
В результате, активная нагрузка подключена к конденсатору и питается от него, конденсатор разряжается. Выходное напряжение MEG-а переходит через ноль (равно нулю), диоды закрыты обратным напряжением с конденсатора и отсекают выходную обмотку от нагрузки.
Нужно ещё учесть, что ёмкость конденсатора фильтра рассчитывается так, чтобы время его разряда было много больше времени заряда. Не вдаваясь в подробности, можно сказать, что с конденсатором такой ёмкости нагрузка может работать несколько десятков периодов выходного напряжения (в данном случае MEG-а). Но зарядить его можно за один-два периода.
В нашем случае нагрузка постоянно питается энергией, накопленной в конденсаторе, и только в моменты максимума (почти) амплитуды подключается через диоды к выходной обмотке. При этом подзаряжается конденсатор. И так в каждом полупериоде.
Итак, при увеличении амплитуды напряжения на выходной обмотке, диоды остаются закрытыми до тех пор, пока амплитуда не превысит (примерно на вольт) напряжение конденсатора. Только тогда диоды откроются и выходное напряжение 'подпитает' нагрузку и подзарядит конденсатор. Так как выходное напряжение фильтра почти равно амплитудному значению выходного напряжения, то и подключение нагрузки будет происходить в моменты максимальной амплитуды выходного напряжения.
Подзарядившись, конденсатор будет продолжать питать нагрузку, а выходное напряжение MEG-а, пройдя через максимум начнёт уменьшаться, диоды закроются, опять отсекая выходную обмотку от нагрузки.